N-Queens I&II

2016-01-10

经典的八皇后问题的延伸，利用回溯算法可以轻松求解，文中还给出了另外一种利用位图（bit manipulations）的做法。

问题描述

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle.
Each solution contains a distinct board configuration of the n-queens’ placement, where ‘Q’ and ‘.’ both indicate a queen and an empty space respectively.

思路

方法一：
经典的回溯问题，我们可以定义一个一维数组int x[n]来表示第i行，我们把皇后放在了第x[i]列。所以当判断第k行，我们把皇后放在x[k]是否合理，我们可以如下判断:

该列上是否有其她皇后
斜率为1的直线上是否有皇后
斜率为-1的直线上是否有皇后

注意：判断斜率为1和-1的直线时，利用求直线斜率的公式，转变为：

$$
|i - k| == |x[i] - x[k]|
$$

bool isSafe(int k){
    int i;
    //方便理解，我们的i从1开始
    for (i = 1; i < k; i++){
        if(x[i] == x[k] || abs(i - k) == abs(x[i] - x[k]))
        return false;
    }
    return true;
}

方法二：

利用 bit manipulations 求解，首先定义了三个向量：

row：为1的地方说明不能放皇后
ld：斜率为1的直线，为1的地方说明不能放皇后
rd：斜率为-1的直线，为1的地方说明不能放皇后

核心： available = board & （~（row | ld | rd））

board 为111…111（n个1）

简单的例子示意图（4皇后）：

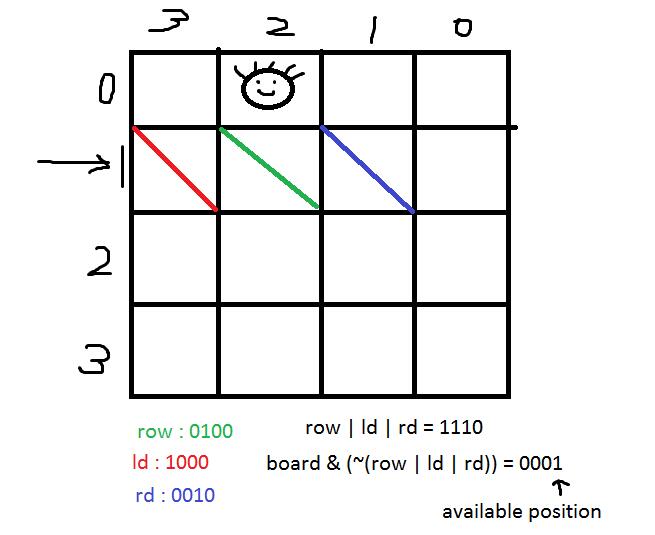
求出可放位置后，经过转换，到下一步：

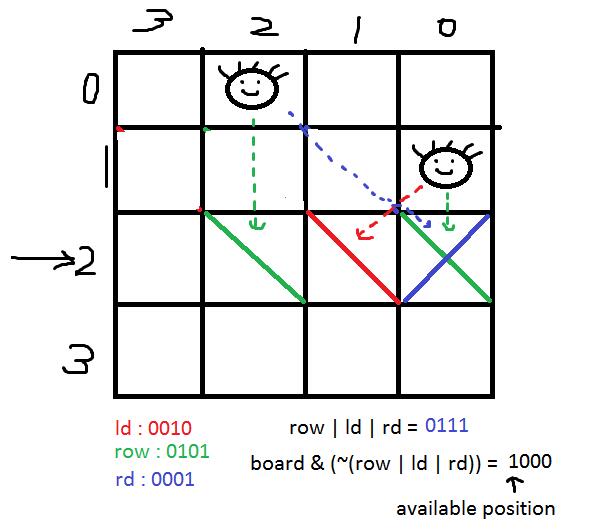
Code

方法一：

bool isSafe(int k, vector<int> &x){
        int i;
        for (i = 1; i < k; i++){
            if (x[i] == x[k] || abs(i - k) == abs(x[i] - x[k])){
                return false;
            }
        }
        return true;
    }
    int totalNQueens(int n) {
        vector<int> x(n+1, 0);
        int cnt = 0;
        int k = 1;
        
        while(k >= 1){
            x[k] = x[k] + 1;
            
            while(x[k] <= n && !isSafe(k, x)){
                x[k] = x[k] + 1;
            }
            
            if (x[k] <= n && k == n){
                //全部行都顺利放完
                cnt++;
            }
            else if (x[k] <= n && k < n){
                //放下一行
                k++;
            }
            else{
                //开始回溯
                x[k] = 0;
                k--;
            }
        }
        
        return cnt;
        
    }

方法二：


int board = 0;    // All available columns to place queens
int cnt = 0;
// row: row constraint
// ld: left diagonal constraint
// rd: right diagonal constraint
void DFS(int row, int ld, int rd) {
    if(row == board) {
        ++cnt;
        return;
    }
    int avail = board & (~(row | ld | rd));   // Available positions
    while(avail != 0) {   // Separately try every available positions 
        int pos = avail & (-avail);  // Extract every possible position
        avail -= pos;
        DFS(row | pos, (ld | pos) << 1, (rd | pos) >> 1);    // Add constraint for row, ld, rd
    }
}
int totalNQueens(int n) {
    board = (1 << n) - 1; //initial the available place.
    DFS(0, 0, 0);
    return cnt;
}